Learn to Survive with Titanic Dataset

In this tutorial, we will learn about one of the most popular datasets in data science. It will give you idea about how to analyze and relate with real conditions.

The Challenge

The sinking of the Titanic is one of the most infamous shipwrecks in history.

On April 15, 1912, during her maiden voyage, the widely considered “unsinkable” RMS Titanic sank after colliding with an iceberg. Unfortunately, there weren’t enough lifeboats for everyone onboard, resulting in the death of 1502 out of 2224 passengers and crew.

While there was some element of luck involved in surviving, it seems some groups of people were more likely to survive compared to others.

In this challenge, we will need to build a predictive model that answers the question: “what sorts of people were more likely to survive?” using passenger data (ie name, age, gender, socio-economic class, etc).

This post will help you start with data science and familiarize yourself with Machine Learning. The competition is simple: use machine learning to create a model that predicts which passengers survived the Titanic shipwreck.

A. Variable Information here

PassengerId is the unique id of the row and it does not have any effect on target

Survived is the target variable we are trying to predict (0 or 1):

  1 = Survived

  0 = Not Survived

Pclass (Passenger Class) is the socio-economic status of the passenger and it is a categorical ordinal feature which has three unique values (1, 2 or 3)

Name, Sex and Age are self-explanatory

SibSp is the total number of the passengers' siblings and spouse

Parch is the total number of the passengers' parents and children

Ticket is the ticket number of the passenger

Fare is the passenger fare

Cabin is the cabin number of the passenger

Embarked is port of embarkation and it is a categorical feature which has 3 unique values (C, Q or S):

  C = Cherbourg

  Q = Queenstown

  S = Southampton

Variable Notes

Pclass: 1st = Upper  2nd = Middle  3rd = Lower

SibSp: The dataset defines relationship as, Sibling = brother, sister, stepbrother, stepsister

Spouse = husband, wife (mistresses and fiancés were ignored)

Parch: The dataset defines relationship as, Parent = mother, father

Child = daughter, son, stepdaughter, stepson

Some children travelled only with a nanny, therefore parch=0 for them.

Below are the few questions we would like to answer after our analysis

• Is there any relation between given info of passengers and their survival?
• What is the survival rate for different age groups?
• Was preference given to women and children for saving?
• Did having higher social status help people improve survival chances?
• What are the effects of being alone or with family?
• Was the survival rate affected by passenger class
• Can we predict if a passenger survived from the disaster with using machine-learning techniques?

Let's Get Started

# importing basic libraries

  import warnings

  warnings.filterwarnings('ignore')

  import pandas as pd

  import numpy as np

  import matplotlib.pyplot as plt

  import seaborn as sns

  import plotly as ply

  from scipy import stats

  import math

# reading the titanic train and test data

  train = pd.read_csv('https://bit.ly/kaggletrain')
  test = pd.read_csv('https://bit.ly/kaggletest')
  train.shape  # (891,12)
  test.shape   # (418,11)

We can check the data head to see what kind of variables we have. Mainly we have two kinds of variables i.e. continuous and discrete.

Here Survived is our target variable, so we save it in the variable y and save the PassengerID for sake of result submission on kaggle.

  y = train['Survived']

  testpassenger = test['PassengerID']

We also drop the passenger id, as it is unique for each record and doesn't contribute anything for survival prediction. Also concatenate the train and test into one for the ease of performing EDA and missing value operation and feature engineering.

  train = train.drop('PassengerId', axis = 1)

  test = test.drop('PassengerId', axis = 1)

  total = pd.concat([train, test], axis = 0, sort=False).reset_index(drop=True)

# Saving variables into different lists

  cat_var = ['Pclass','Sex','SibSp','Parch','Embarked']    #  categorical
  target = ['Survived']                                                      #  target

  con_var = ['Age','Fare']                                                #  continuous

B. Visualization

To plot categorical variables:

def catplot(x, df):

    fig, ax = plt.subplots(math.ceil(len(x)/3), 3, figsize = (20,10))

    ax = ax.flatten()

    for axes, cat in zip(ax, x):

        if cat == 'Survived':

            sns.countplot(df[cat], ax = axes)

            axes.set_ylabel('Count', fontsize=12)#, weight='bold')

        else:

            sns.countplot(df[cat], hue='Survived', data = df, ax = axes)

            axes.legend(title='Survived ?', labels = ['No','Yes'], loc= 'upper right')

            axes.set_ylabel('Count', fontsize=12)#, weight='bold')

catplot(target + cat_var, total)

To plot the continuous variables:

def cont(x, df):

    fig, ax = plt.subplots(1,3, figsize = (18,4))

    sns.distplot( df[df[x].notna()][x] , fit = stats.norm, ax = ax[0], bins = 12)

    # the fit parameter in distplot fits a function of distribution passed in argument

    stats.probplot( df[x].fillna(df[x].median()), plot=ax[1])

    

    sns.boxplot(y = df[x], ax = ax[2])

    plt.show()

cont('Age', total)

cont('Fare', total)

Density plots:

For Age and Fare variables we make density plots, to see if they have any impact on the survival

plot_con = ['Age','Fare']

for i in plot_con:

    plt.figure(figsize=(12,4))

    sns.distplot(train[train['Survived']==0][i], color='r', bins = 5)

    sns.distplot(train[train['Survived']==1][i], color='g', bins = 5)

    plt.legend(title='Survived vs '+i, labels = ['Dead','Alive'], loc='upper right')

    plt.show()

• People with lower age survived more
• It can be concluded that higher fare leads to better survival chance, the binning of fare might improve decision boundary.
• However that relationship might be result of other variables also.

C. Feature Engineering

Now our next steps will be towards feature engineering

1. Feature Engineering - Name:

After a glimpse we can see that name itself cannot help us in any way, so we extract new variables from it i.e. Title and Last Name.

  def map_title(x):

      if x in ['Mr']:

          return 'Mr'

      elif x in ['Mrs', 'Mme']:

          return 'Mrs'

      elif x in ['Miss', 'Mlle', 'Ms']:

          return 'Miss'

      # Master taken separate as all have children age

      elif x in ['Master']:

          return 'Master'

      elif x in ['Col','Capt','Major','Dr','Rev']:

          return 'Staff'

      elif x in ['Don','Lady','Sir','the Countess','Jonkheer','Dona']:

          return 'VIP'

  def feature_name(df):

      df['LastName'] = df['Name'].apply(lambda x:x.split(',')[0])

      df['title'] = df['Name'].apply(lambda x:x.split(', ')[1].split('.')[0])

      df['title'] = df['title'].apply(map_title)

      return df

  total = feature_name(total)

The above functions extracts the features 'title' and 'LastName'.

2. Feature Engineering - Family Size:

The features 'SibSp' and 'Parch' can be combined into one to give family size. Also we create two more features 'IsAlone' and 'FamilyAttrib'.

  def family_size(x):

      if x<2:

          return 'Alone'

      elif x<5:

          return 'Small'

      elif x<8:

          return 'Medium'

      else:

          return 'Large'

    

  def feature_family(df):

      df['FamilySize'] = df['SibSp'] + total['Parch'] + 1

      df['IsAlone'] = df['FamilySize'].apply(lambda x: 1 if x==1 else 0 )

      df['FamilyAttrib'] = df['FamilySize'].apply(family_size)

    

      return df

  total = feature_family(total)

The above functions extract features 'FamilySize', 'IsAlone' and 'FamilyAttrib'.

The next feature we extract is a bit less intuitive. Below is the map of titanic cruise ship deck and cabins.

3. Feature Engineering - Cabin:

The features we extract from Cabin are 'Cabin_Information' and 'Deck'.

  def feature_cabin(df):

      df['Cabin'].fillna("No", inplace=True)

      df['Cabin_Information'] = df['Cabin'].apply(lambda x: "Yes" if x !="No" else "No")

      df['Deck'] = df['Cabin'].apply(lambda x: x[0] if x !="No" else x)

      df['Deck'] = df['Deck'].replace({'T':'A'})

      # cabin T has Pclass 1, hence replaced with A

    

      return df

  total = feature_cabin(total)

The above function extracts features 'Cabin_Information' and 'Deck'.

Do the variables we created, really help???

We also need to check whether the variables added in the above steps are really contributing to survival prediction or not. There are two ways of doing this statistical method and visualization methods. For the sake of simplicity in this post I will only show the visualization method here.

# The survival rate by feature

  def survivalrate(x, df):

      fig, ax = plt.subplots(math.ceil(len(x)/3),3, figsize = (16,8))

      ax = ax.flatten()

      for cat, axes in zip(x, ax):

          pd.crosstab(df[cat], df['Survived'],

                                         normalize='index').plot.bar(stacked=True, ax = axes)

          axes.legend(title='Survived ?', labels = ['No','Yes'], loc= 'upper right')

          axes.set_ylabel('Percentage(%)', fontsize=12 )

      ax[-1].axis('off')    # hide the subplot not used

      plt.show()

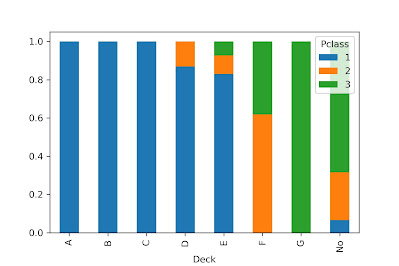
• Deck B, C, D and E have maximum survival rate
• Being alone decreased the survival chances
• Larger family size decreased odds of survival significantly
• Title 'Master' and 'Mrs' have best whereas 'Mr' has worst survival rate respectively

# The survival count of passengers by feature

  def featureplot(x, df):

      fig, ax = plt.subplots(math.ceil(len(x)/3), 3, figsize = (16,8))

      ax = ax.flatten()

      for axes, cat in zip(ax, x):

          if cat == 'Survived':

              sns.countplot(df[cat], ax = axes)

          else:

              sns.countplot(df[cat], hue='Survived', data = df, ax = axes)

              axes.legend(title='Survived ?', labels = ['No','Yes'], loc= 'upper right')

              axes.set_ylabel('Count', fontsize=12)

      

      ax[-1].axis('off')

      plt.show()

• The family size 1 has highest survival count but lowest rate
• The count of male passengers survived is very less
• B, C, D and E decks have more survived than dead

Pclass and Deck passenger count bar plot:

  pd.crosstab([total['Deck']],total['Pclass'], normalize='index').plot.bar(stacked=True)

D. Missing Values Treatment

Visualizing missing values in the dataframe

  fig, ax = plt.subplots(1, 2, figsize=(16, 5))

  sns.heatmap(train.isnull(), cbar = False, 

                                         cmap='inferno', ax = ax[0], yticklabels=False)

  sns.heatmap(test.isnull(), cbar = False, 

                                         cmap='inferno', ax = ax[1], yticklabels=False)

  ax[0].set_xticklabels(train.columns, rotation = 90)

  ax[1].set_xticklabels(test.columns, rotation = 90)

  plt.show()

1. Filling missing values for Age column

We use median age after grouping by Pclass and Sex of passenger

  def fill_age(df):

      df['Age'] = df.groupby(['Sex','Pclass'])['Age'].apply(lambda x:x.fillna(x.median()))

      return df

  

  total = fill_age(total)

2. Filling missing values for Fare column

We use the median fare after grouping by Pclass and Sex of passenger

  def fill_fare(df):

      df['Fare']=df.groupby(['Sex','Pclass'])['Fare'].apply(lambda x:x.fillna(x.median()))

      return df

  total = fill_fare(total)

3. Filling missing values for Embarked Column

We use the location where the maximum passengers boarded i.e. 'S'

  def fill_embark(df):

      df['Embarked'] = df['Embarked'].fillna(df['Embarked'].mode()[0])

      return df

  

  total = fill_embark(total)

In next step will we create bins for the Age and Fare columns in order to enhance the survival classification.

  def age_bin(df):

      bins = [0, 2, 18, 35, 65, np.inf]

      label = [0,1,2,3,4,5]

      df['Age_Bin'] = pd.cut(total['Age'], bins = bins, labels = label )

      return df

  total = age_bin(total)

  

  def fare_bin(df):

      bins = [-1, 7.91, 14.454, 31, 99, 250, np.inf]

      label = [0, 1, 2, 3, 4]

      df['Fare_Bin'] = pd.cut(total['Fare'], bins = bins, labels = label )

      return df

  

  total = fare_bin(total)

I have intuitively, using visualization created the bins. But we can also use quartile bins creation using pd.qcut, which will give close results as above bins.

Finally, we are done with the task of visualization, feature engineering and treating the missing values. Now we get to the easy part of modelling and predicting the outcome on our test dataset.

E. Data Pre-processing

Machine Learning algorithms only understand numbers, so before we get to the model building part, we need to one-hot encode the categorical columns and drop some redundant columns.

You can also use a heatmap to check the new feature set correlation with the target and each other.

  final = total.drop(['Survived','Name','Age','Fare','Cabin',

                                                                'Ticket','LastName','Deck'], axis = 1)

  final = pd.get_dummies(final, columns=['Pclass','Sex','Embarked','IsAlone',

                                                                'FamilyAttrib','title','Cabin_Information'

                                                                ,'Age_Bin','Fare_Bin'] ,

                                                               drop_first=True)

In the model building process, LastName and Deck didn't seem to add any information so dropped them.

Separating the train and test data

  n_train = 891            # number of rows in the train data

  newtrain = final.iloc[:n_train,:]

  newtest = final.iloc[n_train:,:]

# importing the libraries

  from sklearn.model_selection import train_test_split

  from sklearn.metrics import classification_report, roc_auc_score, roc_curve

  from sklearn.ensemble import GradientBoostingClassifier,

                                                   RandomForestClassifier,VotingClassifier

  from sklearn.model_selection import GridSearchCV

  from catboost import CatBoostClassifier    # !pip install catboost

  from xgboost import XGBClassifier            # !pip install xgboost

We also create a model evaluation function for our ease

  def model_eval(model, x_train, y_train, x_test=None, y_test=None):

      print('The model evaluation results')

      model.fit(x_train,y_train)

      train_pred = model.predict(x_train)

      print(classification_report(y_train, train_pred))

      print('roc train :', roc_auc_score(y_train, train_pred))

      print("---------------------------------------------------------------------")

      if x_test:

          print('Predicting for test set')

          test_pred = model.predict(x_test)

          print(classification_report(y_test, test_pred))

          print('roc test :', roc_auc_score(y_test, test_pred))

F. Model Building:

For the prediction we will be using different models.

    1. Gradient Boosting Classifier

    2. Random Forest Classifier

    3. Catboost Classifier

    4. Voting classifier (uses stacked results of already tuned models)

1. model_cat = CatBoostClassifier()
2. model_gb = GradientBoostingClassifier()
3. model_rf = RandomForestClassifier()
4. Voting classifier, here we provide a list of tuples with named instances of models

    clf1 = GradientBoostingClassifier()

    clf2 = CatBoostClassifier()

    clf3 = RandomForestClassifier()

    voting = VotingClassifier([ ('gb',clf1) , ('cb',clf2) , ('rf',clf3) ] )

Model Evaluation:

  model_eval(model_gb, newtrain, y)

We can also use train-test split to check the overfitting/underfitting of the model.

A larger difference in the train and test roc_auc indicate model overfitting on train data as a result making test predictions less accurate.

Further, train and test split can be used to evaluate the model.

  from sklearn.model_selection import train_test_split

  x_train, x_test, y_train, y_test = train_test_split(newtrain, y, 

                                                                          train_size = 0.8, random_state= 42)

  model_eval(model_gb, x_train, y_train, x_test, y_test)

Feature Importance:

  plt.figure(figsize = (16, 4))

  plt.bar(newtrain.columns, model_gb.feature_importances_)

  plt.xticks(rotation=90)

  plt.show()

Can we go further and improve the results ???

GridSearchCV is one of the methods to tune hyperparameters and improve model learning and at the same time reduce overfitting. The above basic models gave pretty good results, but to improve results tuning of the model hyperparameters is very important. For the above models tuning has been performed for the below parameters 

params = {

    'learning_rate':[0.9,0.10, .11, 0.12, 0.13],

    'n_estimators':[200, 300, 350,400],

    'max_depth':[4,5,6,7,8]

}

grid = GridSearchCV(model_cat, params, n_jobs=-1, cv=3)

grid.fit(x_train, y_train)

grid.predict(x_train)

Note: cv=3 indicates 3 fold cross validation of model for each of the hyperparameter combinations.

Predicting the survival of Passengers

  survival_pred = pd.Series(model_gb.predict(newtest))

  submit = pd.DataFrame({'PassengerId':testpassenger , 'Survived':survival_pred})

  submit.to_csv('model_gb.csv', index=False)

Above is a sample code to predict and save the results.